Reading Aloud in Math Class

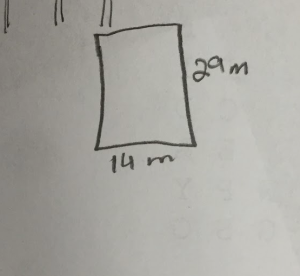
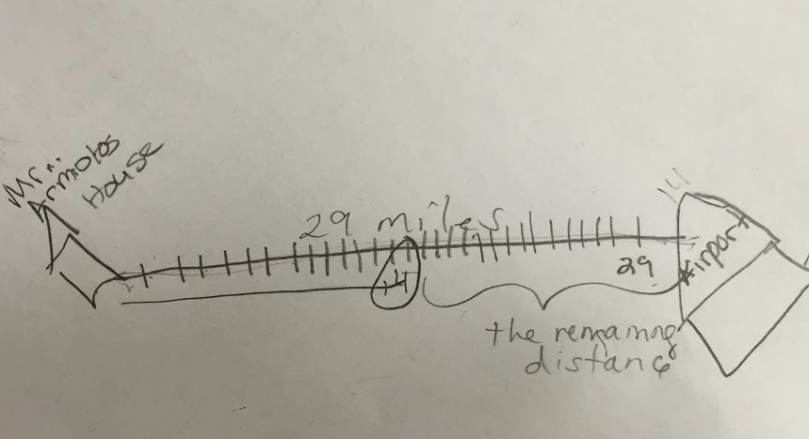
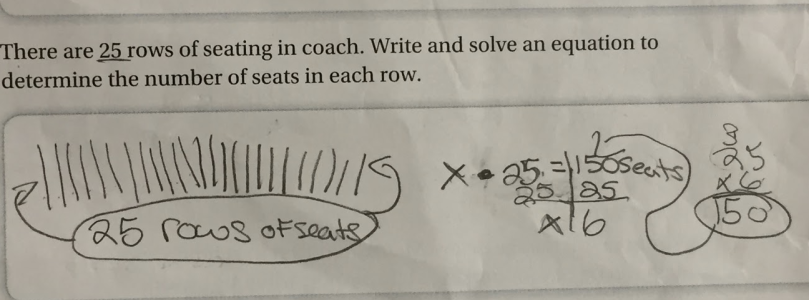So I’ve been informally experimenting with the effect of reading aloud in math class.

Many years ago, I noticed that when a student couldn’t get started on a task on their own, they’d raise their hand and claim “I don’t know what to do.”  I would ask, “Well, what did the problem say?”  The student would then answer, “I don’t know.”  My next step would then be to read the problem aloud and ask “What do you think you’re supposed to do?”  The student would respond to this question…and most often with the correct response.

I didn’t need to ask the students any questions related to the math at hand.  They just needed to hear the problem aloud.

I started to pay attention to this back and forth that I would have with countless numbers of students.  And then began to explore the question-what if they read aloud to themselves???

An eight grade honors level student came to find me because she couldn’t figure out a problem she had on an assignment.  I said read the problem.  She said “I already did.”  I asked her to read it aloud to me.  I could see the lightbulb go off when she finished and she asked “Am I supposed to _______?” And she was correct!

Two nights ago, my fourth grader that was accepted into the STEM program in our district, was working on an online assignment in the other room.  He came out to my husband and I and asked for help because he was stuck.  He sat down next to my husband and began reading the problem out loud to him.  As soon as he finished, he said, “Oh, never mind! I know what to do.”

I’ve noticed that I will often put my fingers on my ears and read-aloud in a whisper if I’m trying to double check the words that I’ve written.  It’s helpful to hear myself.  How can we explore this more with students?  How can we incorporate this in our classrooms?

I did a quick search attempting to find research on this topic.  I noted this article about reading aloud for English language learners.  But what was interesting was this:

---

I’m interested in researching this further and would definitely love to know if anyone has had similar experiences with their students.

Learning from a 5th Grade Math Team

When my oldest child entered kindergarten I wanted a way to volunteer my time at the school, so I began coaching the 5th grade math team.  I saw this as an opportunity to better understand the math that elementary students bring with them to middle school. The elementary school that my children attend is a feeder school to my middle school.

I used the set of resources provided by the school system to train my mathletes that year. One problem I tasked them with was titled Kicking Tees below:

I didn’t attempt this problem before giving it to the students that day.  I watched as they solved it…easily handling #1, skipping #2, and then answering #3.  In my mind I thought, “Wow! I’d create an equation to solve #2…how would a 5th grader figure this out?”

I can’t be too dissimilar from other secondary certified teachers, where an algebraic approach is the first that comes to mind.  It took me a few moments to think about using a table, or simply guessing and testing given the boundaries offered by the answers to #1 and #3.

This was a revelation for me though…That students might have skills to approach problems in which I’d use a more sophisticated method.

I was curious about what a 7th grade Algebra class in the midst of learning about systems of equations might do with this problem.

They did the EXACT same thing that the 5th graders did~they skipped #2!

This began my thinking about the intersection between the teaching of content, skill, and strategy.  And the connection between elementary math and algebraic thinking.

I used this problem solving experiment to talk with the 7th grade students about math learning and about the connection between arithmetic and algebra.

For teachers, this highlights the importance of horizontal content knowledge…

“a kind of mathematical ‘peripheral vision’ needed in teaching, a view of the larger mathematical landscape that teaching requires”

“According to Ball and Bass (2009), HCK is an awareness of where and how the mathematics being taught fits into the structures and hierarchies of shared collective mathematical knowledge. This awareness serves both to engage students and to provide meaning to the present mathematical experience”

Further, this article reports

“The teachers in our study seemed to be more concerned about the mathematical content at the level they were teaching than the broader (more advanced) mathematical context—which can be referred to as the mathematical horizon”

---

It’s become incredibly important for me in the work that I do with teachers, to help them see how the math that they are teaching fits into the learning the students do across a mathematical spectrum.

…in addition to helping teachers see the importance of this “horizontal content knowledge” as a way to create instruction that engages, inspires, and makes math a meaningful, connected body of work.

 

Mosvold, R., & Fauskanger, J. (n.d.). Teachers’ Beliefs about Mathematical Horizon Content Knowledge. Retrieved May 27, 2016, from http://www.cimt.plymouth.ac.uk/journal/mosvold2.pdf

 

We Need More Drawing in Math Class

I worked with a 6th grade student in our In School Intervention classroom today.  I do this every day.  A boy had been assigned a set of pages from a workbook and had begun the work on his own. From what he had already completed, I could tell that this student had a strength in math. He was unsure of what he had done, so he was looking for validation from me.  We looked at this next problem together:

He said, “so you gotta subtract right?” I said, “yes you do, but that’s if you’re looking for the answer. This is asking you to write an equation.”

He began to write y = x – 14.

I talked to him about variables, and how many unknowns were in this problem and he could tell that there was only one.

I asked him to draw a picture of the situation.  Here is what he drew.

HMMMM….(maybe they’ve recently worked on area and perimeter???)

I then asked him to reread the problem and prompted him to draw the house and the airport.

He drew the line between the house and the airport, and I had to do some questioning to get him to realize it represented the distance of 29 miles.  We reread the problem and I asked him about the 14 and how he would represent that on the drawing.

He thought to himself for a moment and then began drawing the tick marks.  I could tell that he was counting them.  He labeled the 14th tick mark and the 29th, and then circled the 14.

I drew the bracket and asked him what that would represent.  He said with a questioning tone, “the remaining distance?” Thinking for a minute, he then said, “oh I know…would it be 14 + x = 29?”

We did one more problem together that we represented with a drawing, and then I left him to be independent in the rest of his work.

He came over to show me one of his drawings and the equation he had written:

(In a previous part of the problem they were told there are 150 seats in coach seating.)

We high-fived!

---

Teaching students how to create math drawings is a valuable sense-making tool that can be over looked in math class.  I know numerous reading language arts teachers that ask students to draw pictures to portray what’s going on in a story.  We need more of that in math class.

Teach Math as a Story

 

I had the opportunity recently to complete peer observations outside of my content area. I scheduled a half day of observations with a sixth grade social studies teacher new to our building.  We observed in two eighth grade social studies classrooms and one sixth grade classroom.

If you’ve never observed outside of your content area I highly recommend it.  I think it forced me to pay closer attention to the general instructional practices, rather than focusing in on the content.

In the sixth grade classroom the teacher began by reviewing what the students discussed in the previous class.  They were in the middle of learning about Julius Caesar and the fall of the Roman Republic. The students eagerly answered her questions and were incredibly engaged with the “story” she was telling.

I was engaged with the story, intrigued by the cast of characters and happenings that she described.  The students were making predictions about what would happen next and the teacher responded, “just wait…maybe we’ll see today…”

The students knew the characters in this story, they understood how they related, they recalled the parts of the story that were told to them in the previous class, they made predictions about what would happen next. The teacher also knew this story, oh so well, that she could add on interesting and important details and maintain the curiosity that she had sparked.

I wondered…can we teach math as a story?

I decided to Google “Teach Math as a Story” and the first result was this.

It is an excerpt from a book and it’s mostly about using stories in the math classroom, but it has useful think-a-bouts like this…

“In our description of how to teach mathematics, we are not concerned with fictional stories about the topic, but rather we are concerned with how we can shape the topic to enhance its attraction to students. In doing this, we will not be falsifying anything, or giving precedence to entertaining students over educating them. Instead, we will be engaging them. We see engaging students with mathematical activity as a crucial aspect of successful education as, and it is the real vividness and importance of this subject in which we want to engage students.

In summary, the great power of stories, according to Kieran Egan (1986, 2004, 2008), is in their dual mission: they communicate information in a memorable form and they shape the hearer’s feelings about the information being communicated.”

I did some additional searching through Peter Liljedahl’s work and found this interesting article that seems related to what teacher planning might look like in order to teach math as a story.

In this article, Zazkis and Liljedahl contrast a typical lesson plan to what they’ve termed a lesson play.

“In terms of the pedagogical features of the lesson play, we wish to draw attention to some aspects of its format. The structure of the lesson play – as a dialogue occurring overtime with possibilities for different points of view – allows for the portrayal of the messy, sometimes repetitive interactions of a classroom. This structure stands in stark contrast to a necessarily ordered and simplified list of actions such as: take up homework, state definition, provide examples,give problems, and evaluate solutions.”

Crafting a lesson play provides for the improvised interactions that may occur with teaching math as a story-being able to respond and shift according to responses from students.

---

I don’t think any of this is dissimilar from the ideas in books such as 5 Practices,  but I now have a different analogy that I’m considering. As I continue the thinking that I’ve started here, I want to keep in mind these things in terms of how I work with the math teachers in my building:

1. On the macro level-How can I help teachers to tell the math story as a set of interconnected ideas and concepts?
2. On the micro level-How can I help teachers to consider a lesson play, so that the day to day story is just as interesting as the year long story they are telling? How do we get students to want more?

 

My Favorite Formative Assessment Tasks

I’m a little late…but, here’s my week 2 “My Favorite” post for the Explore MTBoS blogging initiative.

The Charles A. Dana Center out of The University of Texas at Austin has put together a great set of tasks for eliciting student thinking.

One of my favorite tasks that I have used with 8th graders (for years) is called Mosaics.

Because we spend time making sense of the patterns from the Visual Patterns site, this task works well as an independent assessment task.

I particularly like question one in that it asks students to represent the problem in at least three ways–they are not told how to represent the problem.  I like to see if they will use a table, graph, etc.

Also, it’s interesting to see how different students “see” the pattern growing and how they choose to show that thinking.

And my FAVORITE piece of student work for this task incorporated the independent use of “noticing…”

Student did some noticing on her own…Yay! Cc @maxmathforum @MFAnnie pic.twitter.com/US3wJkHPP5

— Bridget Dunbar (@BridgetDunbar) February 24, 2015

---

 

Here is a link to additional student work from this task.  We’ve used this task, along with the student work, as part of our back-to-school professional development on using a examining student work protocol.

Dana Center tasks are not a free resource. You can purchase a book of these tasks here, or on CD here.

Everything I learned about teaching I learned from teaching students with special needs…

I came about a teaching career in a round about way.  As a math major at a small liberal arts college in Southern Maryland, I earned money by tutoring local middle and high school students.  I realized that I really enjoyed this experience and decided to pursue a teaching degree at the graduate level.

While taking classes towards a graduate degree for secondary math instruction, I fell into a job at a non-public special education facility.  I worked under a conditional certificate with some very wonderful special educators.  I ended up becoming THE math teacher for the entire high school program (the Harbour School is a k – 12 facility).  This meant that I taught all of the students ALL of their high school math.

I believe that I wouldn’t be the educator that I am today without this experience.

At the Harbour School I worked with students with all sorts of ABILITIES.  This school was their SAFE HARBOUR.  The students came to the school because it was found that their home school couldn’t meet their educational needs.

Teaching math at this school was an exercise in flexibility.  I had to really listen to the students to understand their understanding.  I do believe that math was a mystery for most.  I’ve always used this analogy for teaching math…

If I couldn’t get through the front door, I found a way in through the window, the garage, or around the back of the house.

By having to ask the right questions and make the right connections, this experience helped me to understand the math I was teaching at a deeper level.

At the Harbour School I also learned:

• acceptance
• tolerance
• patience
• community
• awareness
• perseverance
• resilience

If you are wondering about how to meet the needs of the students in your classroom with learning challenges–my advice is to listen to them.  ...Then figure out how to get into the house…

My favorite talk about listening from @maxmathforum…

July Challenge #11 I’m a Day Behind-A “Few Good Posts”

So I’m a day behind on this challenge…but, I will persist until I make it up.  I REALLY want to respond @mathtans about “Why I Post!” but I’ll do that another time.

Today I want to highlight a few of the bloggers that Google led me to before entering into this world of Twitter and Blogging.  I’m including one of their posts that I particularly like.

• @fawnpnguyen and Deconstructing a Lesson Activity–Part 2 (and Part 1)
• @ddmeyer and The Unengageables (I particulary like @k8nowak ‘s comment here)
• @jreulbach and Square Roots with Cheez-Its
• @samjshah and his Virtual Filing Cabinet
• @robertkaplinsky and Why Does Depth of Knowledge Matter
• @emergentmath and Developing a Taxonomy of Problems

I feel fortunate to have found SOOOOO many more bloggers AND posts that I find valuable since jumping in with both feet!

July Challenge #10 Writing in the Math Classroom

Many years ago I read the book Writing to Develop Mathematical Understanding by David Pugalee.  I want to use this post to record some of the important points.

Pugalee wrote that

“The goal of writing in mathematics is to engage students in ways that require them to think deeply about the mathematics they are encountering.”

He suggested that, writing, or more generally, communication, happens along a continuum.

 

This continuum “is not about writing ability but about the level of cognitive engagement of the student.”

He offers many practical suggestions for incorporating writing into the daily routine of math classrooms.

Beginning of the lesson suggestions (pages 36-38):

• Use a prompt such as “Write what you know about ________.”
• Have students write a short description of how they solved a particular homework problem.

Middle of the lesson suggestions:

• Have students write an example or draw a diagram or other illustration to demonstrate a key idea or concept.
• Have students write a question about a concept or problem, then turn to another classmate and exchange questions.
• If students are taking notes, pause and have them write a summary of an idea or concept in the margin.

End of the lesson suggestions:

• Write the main idea from the day’s lesson.
• Write definitions in your own words. This might also apply to a procedure or property.
• Have students exchange notes, a practice problem, or another task.  Students can identify common elements and approaches as well as differences.

He shares a list of 50 Activities for Writing in Mathematics…a few of my favorites include:

1. Construct test or quiz questions
2. Write freely on any topic
3. Create a dialogue between one student and another
4. Defend a decision or action
5. List characteristics or steps
6. Write a mathematics word problem
7. Prepare an outline of a lesson
8. Identify personal goals for mathematics learning
9. Write about what gave you difficulty on a particular task
10. Write about how two problems are similar or different

Pugalee discusses the importance of creating a safe environment for communicating in the classroom.  He offers suggestions for promoting this culture.

Struggling writers might need “a framework or skeleton” as entry points into a communication task.  This might look like:

I need to…

I notice…

This means…

So, I need to… because…

Therefore, the…

A couple of quick ideas that I use for incorporating writing into lessons that were inspired by this book:

• I might put these words on the board:  hypotenuse, Pythagorean Theorem, leg.  And then ask students to write 2-3 sentences using these words.
• I like to create fill-in the blank responses.  So students have to make sense of what’s already on the paper…and how best to complete the sentences.

There is soooooo much out there on this topic.  But I don’t think enough of it has trickled down to implementation in the classroom.

I’m going to continue to add to this list below…but here are a few additional resources for learning about writing in the math classroom.

• Stop and Jot via ASCD
• Writing in Math (by Marilyn Burns)  via ASCD
• Using Writing in Mathematics to Deepen Student Learning via McREL
• Research Summary:  Writing in Middle Grades Mathematics via AMLE
• Writing in Mathematics via Mathwire

 

 

July Challenge #7 Start with a Simpler Problem

If you haven’t already…Check out The Centre for Education in Mathematics and Computing and their Problems of the Week.

I came across this Problem of the Week below in their book of problems and solutions grades 7/8 for the years 2012-2013.

I modified the task to make it appropriate for the new year 2014.

I planned to use this with a group grade level 8th graders.  I thought it looked like a perfect problem to teach the problem solving strategy of starting with a simpler problem.

Just I had imagined, when I presented them with the problem, they immediately shunned it and put it off by saying they had no idea.  They wanted to try and put it into the calculator (which offers up its own set of learning opportunities).

I asked, “Well, what DO you know?”  Of course they started with is 125.  So, I said well let’s write that down.

Then I asked, “Well, what ELSE do you you know?”  And someone shared is 25.

At this point, we talked about how we organize information in math.

We continued our table, and many students began to recognize the pattern.  I needed to use guiding questions for some to be able to communicate just how the pattern worked.

I think this is a very simple, yet powerful, problem for explicitly teaching a very specific problem solving strategy.

End note:  If you haven’t already read this book…YOU MUST!  It validated many things that I already believed…but gives VERY useful and practical strategies for being explicit about how you teach problem solving.

I’d like to put together a set of tasks that all make use of this problem solving strategy so that students have the opportunity to apply it themselves.

I’d love to hear about how you teach problem solving!

First REAL post…

It’s been a long time since I started this blog b/c of the MTBoS.  I appreciate all of these people who are just so SMART and thoughtful about what they do to improve the lives of kids.

I am finding it hard to figure out what I could have to offer in starting a new blog…I understand and respect the reflective process as an educator, so I can see the benefits for myself.  But, I want to contribute as well…

I thought for this post I would ramble on about my observations of kids and their ability (or “inability”) to make meaning from print themselves.  In my role as an Instructional Resource Teacher I have the unique opportunity to see a great variety of students from grades 6 through 8–below grade level to honors.  I have found that a great many of these students have difficulty even making sense of directions independently.

When I was still in the classroom, teaching on grade level 8 students, it would take just a simple verbal prompt from me (basically reciting what the question was asking)…and students would say “ooh that’s all it (the question) wants me to do?”  There could be some learned helplessness in there…but I think that we (math teachers) could do more to help students become better math “comprehend-ers”!!

What does this look like???  When I began to hear the discussion  among ELA teachers at my school re: annotating text (according to Common Core), I thought…WOW!  That could be a useful tool in the math classroom…put the thinking aloud that I usually do with them as I’m teaching–on paper…link it to the print in a concrete way.

I had a Twitter conversation with @JustinAion and @cheesemonkeysf re: just this topic…

@cheesemonkeysf @JustinAion @reilly1041 @crstn85 my son's elem says "leave tracks of your thinking" #annotationnation 😉

— Bridget Dunbar (@BridgetDunbar) October 30, 2013

The ELA teachers in your building should have a process that the kids are used to.  If you ask them (the kids)…they will tell you that they are annotating in their ELA class (if you are a Common Core state).

There is still a lot to discuss here…but I want to add one more great share by @lsquared76:

https://twitter.com/lsquared76/status/394982935872294912

I retyped it up for a 6th grade class using a task from @IllustrateMath:

@lsquared76 @JustinAion @crstn85 @Mythagon @IllustrateMath Try this again…I pdf'd the doc: http://t.co/bwbPcyPbMq

— Bridget Dunbar (@BridgetDunbar) November 4, 2013

I was able to use this in a 6th grade accelerated class (the teacher and I co-teach…he lets me try things).  On this very first go around…I felt like the kids did well with the summarize questions on the left (remember these are the high kids though).  However, articulating a plan (the part on the right) gave them some trouble.  It did allow us to see the divergent thinking about how to solve the problem (which students recognized division of fractions vs repeated subtraction)…and then move into a discussion of efficient strategies.  We will use this model again and collect more data.

So…this is my first “real” post…I have more I want to offer on this topic.  But, I just felt like I needed to get this first one under my belt!

Thanks to the twitter folk that I mentioned here!  *and @algebrainiac for helping with my embed issues!!  😉