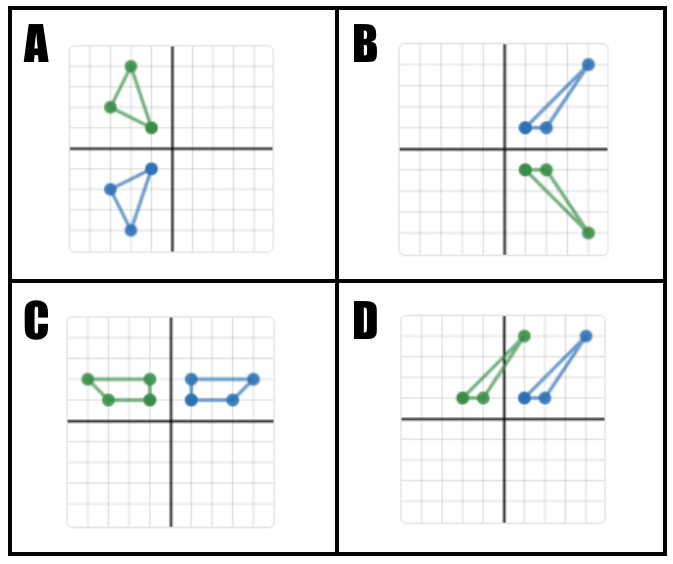
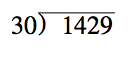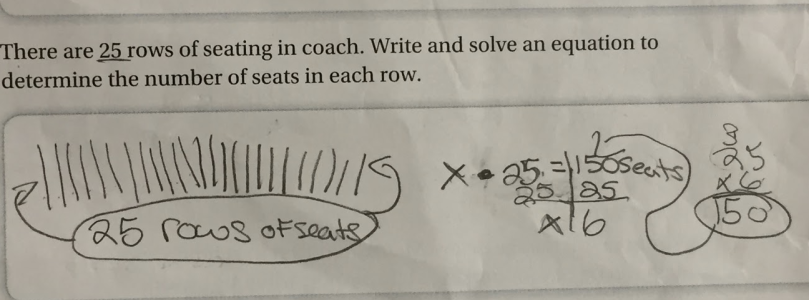When my oldest child entered kindergarten I wanted a way to volunteer my time at the school, so I began coaching the 5th grade math team. I saw this as an opportunity to better understand the math that elementary students bring with them to middle school. The elementary school that my children attend is a feeder school to my middle school.
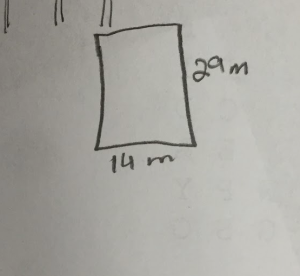
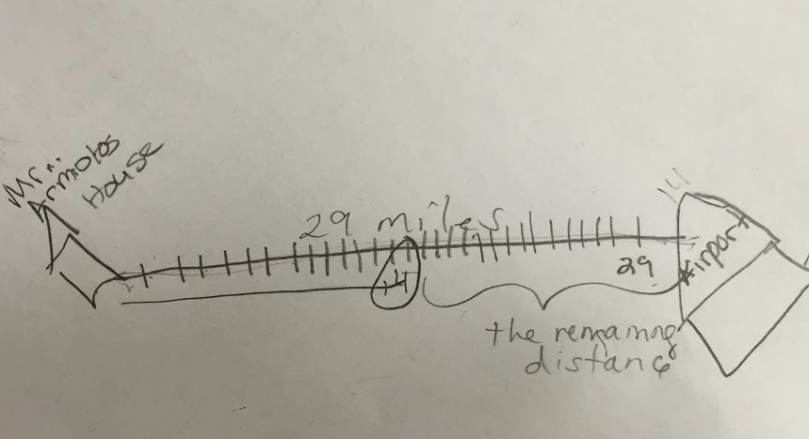
I used the set of resources provided by the school system to train my mathletes that year. One problem I tasked them with was titled Kicking Tees below:

I didn’t attempt this problem before giving it to the students that day. I watched as they solved it…easily handling #1, skipping #2, and then answering #3. In my mind I thought, “Wow! I’d create an equation to solve #2…how would a 5th grader figure this out?”
I can’t be too dissimilar from other secondary certified teachers, where an algebraic approach is the first that comes to mind. It took me a few moments to think about using a table, or simply guessing and testing given the boundaries offered by the answers to #1 and #3.
This was a revelation for me though…That students might have skills to approach problems in which I’d use a more sophisticated method.
I was curious about what a 7th grade Algebra class in the midst of learning about systems of equations might do with this problem.
They did the EXACT same thing that the 5th graders did~they skipped #2!
This began my thinking about the intersection between the teaching of content, skill, and strategy. And the connection between elementary math and algebraic thinking.
I used this problem solving experiment to talk with the 7th grade students about math learning and about the connection between arithmetic and algebra.
For teachers, this highlights the importance of horizontal content knowledge…
“a kind of mathematical ‘peripheral vision’ needed in teaching, a view of the larger mathematical landscape that teaching requires”
“According to Ball and Bass (2009), HCK is an awareness of where and how the mathematics being taught fits into the structures and hierarchies of shared collective mathematical knowledge. This awareness serves both to engage students and to provide meaning to the present mathematical experience”
Further, this article reports
“The teachers in our study seemed to be more concerned about the mathematical content at the level they were teaching than the broader (more advanced) mathematical context—which can be referred to as the mathematical horizon”
It’s become incredibly important for me in the work that I do with teachers, to help them see how the math that they are teaching fits into the learning the students do across a mathematical spectrum.
…in addition to helping teachers see the importance of this “horizontal content knowledge” as a way to create instruction that engages, inspires, and makes math a meaningful, connected body of work.
Mosvold, R., & Fauskanger, J. (n.d.). Teachers’ Beliefs about Mathematical Horizon Content Knowledge. Retrieved May 27, 2016, from http://www.cimt.plymouth.ac.uk/journal/mosvold2.pdf
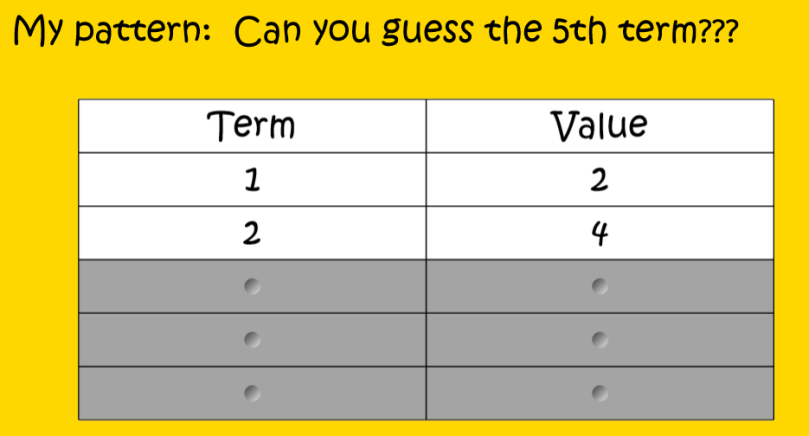
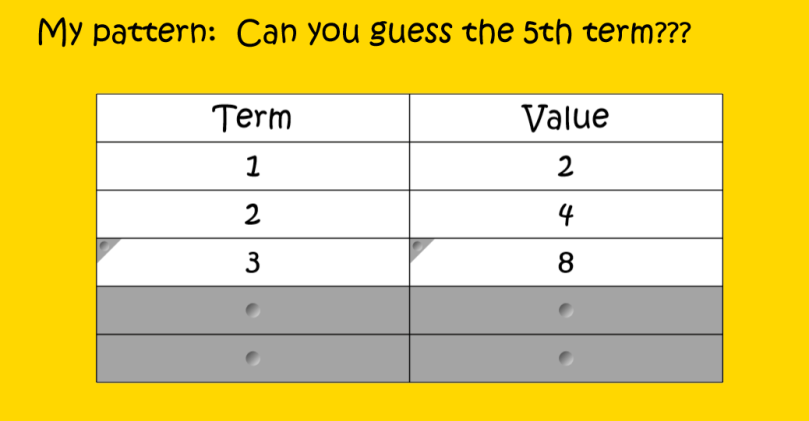
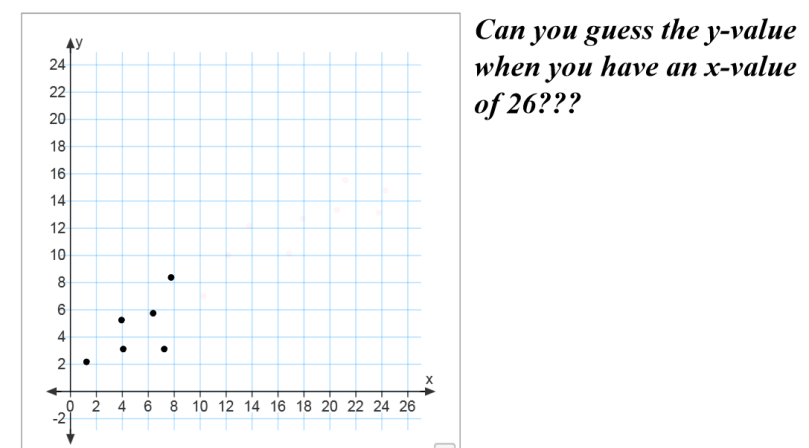
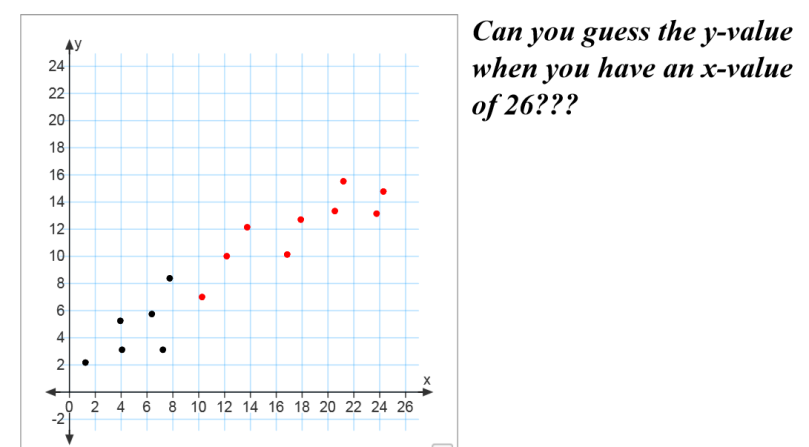
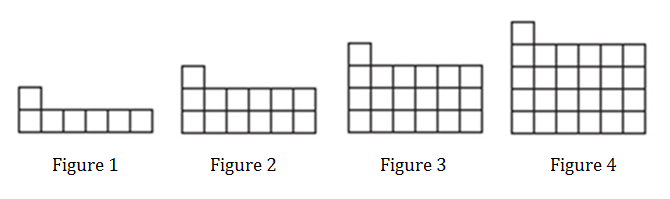 I give them this:
I give them this: 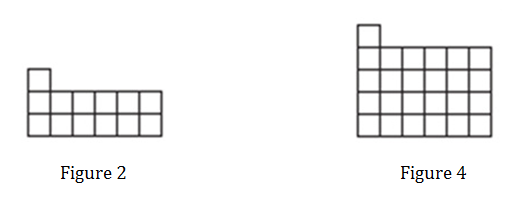 The students work on their dry erase board to create an input-output table of data points beginning with x is 0. We’ve spent A LOT of time creating our own tables that it has really started to become second nature. I didn’t tell them how to figure out the missing figure numbers…they just figured it out on their own…
The students work on their dry erase board to create an input-output table of data points beginning with x is 0. We’ve spent A LOT of time creating our own tables that it has really started to become second nature. I didn’t tell them how to figure out the missing figure numbers…they just figured it out on their own…