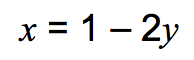Vacas y Pollos ~ Best Day Ever

Yesterday I was talking to our Algebra teacher.  She had asked the Spanish teacher in the building to translate the  problem below so that she could pose it to her students that take both Algebra and Spanish.

Our population of students that are emerging bilingual has grown significantly over the past several years.  The grade 8 students are also working on systems of equations and I had the perfect teacher in mind to pose this problem (written in Spanish) to his students as well.

His last class has the greatest number of Spanish speaking students and I wanted to see the look on their faces when he posted this problem on the board…

Priceless. I watched the biggest smile appear on their faces! The look of joy of what they knew. The boy that participates the least read the problem out loud so quickly and proudly…it was AWESOME! The rest of the students were in awe. They tried to figure out pieces of the problem. But, the students that usually have to spend time using Google translate to figure out what was going on, were the first ones to get to dig in this time.

One girl then said…”wow…they have to do this all the time.”

Yep.

Best day ever.

Un-quiz

My first year out of the classroom was 2010.  I was talking to a colleague today about a type of assessment I used to do in my classroom.  I called it an un-quiz.

This is a variation of a typical multiple choice quiz, except that I asked for a WRONG answer. Along with the wrong answer choice, the students had to give a reason why it was a wrong answer.  (Be sure that your wrong answer choices provide valuable information!) This allowed me to see how they reasoned about wrong solutions, language they used, AND the students had multiple means of showing their knowledge.

I haven’t used this strategy in a while…if you do something similar or try it for the first time, I’d be interested in hearing about what you think.

 

Equal and Opposite

I don’t know if this is the right title for this post…it feels like it is.  I get to its point at the bottom…

I was supporting an 8th grade teacher that was implementing the Classifying Solutions to Systems of Equations formative assessment lesson from Mathematics Assessment Project.

The students had not yet worked with linear equations in any form other than slope-intercept form.  The students already understood the different types of solution a system might have.

The students started out by completing the assessment task.  I wanted to focus on this part below:

I’ve encouraged this teacher to build a strong foundation for students being able to create and complete a table of values.  Creating a table should be a go-to strategy for students if all else fails.

I stood in the back of the room and I looked at the second equation…

I wondered if I could make a connection for kids…if it would be too much, or would they follow…Here is the gist of what I did:

I interrupted the class to pose a question.

Me: What do we know about an equation that is solved for y?

Students: We know the y-intercept and we know the change in y over the change in x.

Me: What do you notice about this equation?

Students: It’s solved for x.

Me: What do you think that might tell you?

Students: The x-intercept???? (Imagine a questioning tone here…) Is that a thing?

Me: Yes it is a thing. What about the coefficient of the y? What do you think that might tell you?

Students: The change in x over the change in y??? (Imagine a questioning tone again)

Me: Yep. Let’s pull up Desmos and check it out.

I remember being a math student that naturally made these sorts of connections~that if something happened mathematically one way, I could predict what would happen in an opposite direction.

I want the students to know and wonder about these things for themselves.  But, I think we need to make it obvious to them sometimes that they can do this thinking on their own.

Teach Math as a Story

 

I had the opportunity recently to complete peer observations outside of my content area. I scheduled a half day of observations with a sixth grade social studies teacher new to our building.  We observed in two eighth grade social studies classrooms and one sixth grade classroom.

If you’ve never observed outside of your content area I highly recommend it.  I think it forced me to pay closer attention to the general instructional practices, rather than focusing in on the content.

In the sixth grade classroom the teacher began by reviewing what the students discussed in the previous class.  They were in the middle of learning about Julius Caesar and the fall of the Roman Republic. The students eagerly answered her questions and were incredibly engaged with the “story” she was telling.

I was engaged with the story, intrigued by the cast of characters and happenings that she described.  The students were making predictions about what would happen next and the teacher responded, “just wait…maybe we’ll see today…”

The students knew the characters in this story, they understood how they related, they recalled the parts of the story that were told to them in the previous class, they made predictions about what would happen next. The teacher also knew this story, oh so well, that she could add on interesting and important details and maintain the curiosity that she had sparked.

I wondered…can we teach math as a story?

I decided to Google “Teach Math as a Story” and the first result was this.

It is an excerpt from a book and it’s mostly about using stories in the math classroom, but it has useful think-a-bouts like this…

“In our description of how to teach mathematics, we are not concerned with fictional stories about the topic, but rather we are concerned with how we can shape the topic to enhance its attraction to students. In doing this, we will not be falsifying anything, or giving precedence to entertaining students over educating them. Instead, we will be engaging them. We see engaging students with mathematical activity as a crucial aspect of successful education as, and it is the real vividness and importance of this subject in which we want to engage students.

In summary, the great power of stories, according to Kieran Egan (1986, 2004, 2008), is in their dual mission: they communicate information in a memorable form and they shape the hearer’s feelings about the information being communicated.”

I did some additional searching through Peter Liljedahl’s work and found this interesting article that seems related to what teacher planning might look like in order to teach math as a story.

In this article, Zazkis and Liljedahl contrast a typical lesson plan to what they’ve termed a lesson play.

“In terms of the pedagogical features of the lesson play, we wish to draw attention to some aspects of its format. The structure of the lesson play – as a dialogue occurring overtime with possibilities for different points of view – allows for the portrayal of the messy, sometimes repetitive interactions of a classroom. This structure stands in stark contrast to a necessarily ordered and simplified list of actions such as: take up homework, state definition, provide examples,give problems, and evaluate solutions.”

Crafting a lesson play provides for the improvised interactions that may occur with teaching math as a story-being able to respond and shift according to responses from students.

---

I don’t think any of this is dissimilar from the ideas in books such as 5 Practices,  but I now have a different analogy that I’m considering. As I continue the thinking that I’ve started here, I want to keep in mind these things in terms of how I work with the math teachers in my building:

1. On the macro level-How can I help teachers to tell the math story as a set of interconnected ideas and concepts?
2. On the micro level-How can I help teachers to consider a lesson play, so that the day to day story is just as interesting as the year long story they are telling? How do we get students to want more?

 

A Round Up of Posts on Professional Development

As an Instructional Coach one of the favorite things that I do is plan professional development.  However, it also produces such great anxiety because we all know how most of our colleagues feel about sitting through another round of professional development.   Professional development shouldn’t feel like something that is done to you…it should be done with you.  I realized that there are some great posts by those that deliver professional development and I wanted to round them up here.

 

Wrapping Up A Year Of Math Intervention PD  by @bstockus

This means having a skill set that allows you to adapt and customize as needed to help the children grow mathematically, not to follow some prescription as though we’re trying to cure a cold.

Professional Development:  Doing Mathematics by @NicoraPlaca

My goal is that through experiencing math this way, teachers will see a benefit to this way of learning–that when we have the experience of seeing why a formula works or how it works, we have a different experience, which leads to a different type of understanding.

Changing Our Practice, Slowly by @jwilson828

When are we going to realize that over the past few years teachers have been making efforts to change their classroom instruction from students “sitting and getting” to students actively engaging in the mathematics?

I Did Professional Development All Wrong by @davidwees

So instead of spending the entire time I present talking, I give participants much more opportunity to talk. Instead of participants sitting around listening, I give them opportunities to do.

Establishing a Culture of Learning…The First Hour by@MathMinds

A culture where teachers talk about instruction, math problems, and student ideas, feel ownership in their lessons and the lessons of others, and can comfortably visit one another’s classrooms.

 

---

 

And because I value this bigger view on the current state of professional development…

Professional Development is Broken, But Be Careful How We Fix It by @tchmathculture

As long as we don’t have strong frameworks for understanding how teachers learn, PD –– even localized, teacher-led PD –– risks being just another set of activities with little influence on practice.

My Favorite Formative Assessment Tasks

I’m a little late…but, here’s my week 2 “My Favorite” post for the Explore MTBoS blogging initiative.

The Charles A. Dana Center out of The University of Texas at Austin has put together a great set of tasks for eliciting student thinking.

One of my favorite tasks that I have used with 8th graders (for years) is called Mosaics.

Because we spend time making sense of the patterns from the Visual Patterns site, this task works well as an independent assessment task.

I particularly like question one in that it asks students to represent the problem in at least three ways–they are not told how to represent the problem.  I like to see if they will use a table, graph, etc.

Also, it’s interesting to see how different students “see” the pattern growing and how they choose to show that thinking.

And my FAVORITE piece of student work for this task incorporated the independent use of “noticing…”

Student did some noticing on her own…Yay! Cc @maxmathforum @MFAnnie pic.twitter.com/US3wJkHPP5

— Bridget Dunbar (@BridgetDunbar) February 24, 2015

---

 

Here is a link to additional student work from this task.  We’ve used this task, along with the student work, as part of our back-to-school professional development on using a examining student work protocol.

Dana Center tasks are not a free resource. You can purchase a book of these tasks here, or on CD here.

Thinking about Feedback

There have been some really great posts lately about how teachers are giving feedback on assessments.  You could read this post here by Nathan Kraft or this post here by Fawn Nguyen.  Also, there is a great Teaching Channel video on highlighting mistakes as a grading practice for you to watch here.

All of these posts show the power of the highlighter.

A strategy that I started using last year involves the highlighter…but in a different way.

Problem-Attic  is a resource I’ve been using to create weekly assessments.  I wanted to figure out a way to help students to be more independent in identifying and revising mistakes.

I decided to turn each problem from the assessment into its own one page station where I highlighted important features and made notes of important think-abouts.  For the most part…these related to common misconceptions or careless errors.

Students then had the opportunity to work around the room and read the “hints” that were provided in order to revise their work.  Some of my hints were probably too “hinty,” but it was a starting point for a process that I was working out.

I did this with 8th grade-on grade level students.

Students reported liking the process–and were able to figure out their errors independently of me.

I’m hoping to refine this process this year.

Where’s the Algebra?

You won’t know this, but this is my 2nd draft of this post.  (I even changed the title.)  I went running half way through what I was trying to write and everything that I really wanted to say came to me so clearly. I should have stopped and recorded the words that were so fluidly coming to mind, but I didn’t.

It made me wonder, however, about why the words that I was struggling to string together for the original post came to me so easily while out running.  I decided that my mind was free of the clutter of trying to say the right things and in the right way–allowing me the ability get at the heart of what I wanted to communicate.

This–I decided–is the reason that balance problems are a great way for students to interact with the reasoning of equation solving.  They are free of the clutter of the procedures and notation and get at what is really going on.

Yesterday, I read Michael Pershan’s post about the use of balance problems (which I consider a sort of puzzle) as part of a series on solving equations.

He is able to so clearly articulate all of the reasons that I believe that these sorts of tasks are a valuable tool in reinforcing the thinking of solving equations.  (I would read his post on this because he is really good at thinking through these sorts of things.)

I used this “balance reasoning” that he referred to in order to make the connection between what students know how to do naturally and the skill that I wanted them to walk away from 8th grade being fluent in–solving equations.

8th graders have done a ton of work solving equations, but still, many are not fluent.  I used these puzzles during warm-ups without expecting any sort of equation writing/solving.  Over the course of time…I wanted the students to begin to ask why we were doing them when they were so easy.  I used the balance problems from EDC, but I also made great use of some of the resources found here.

One resource I used from this site is Mystery Numbers.  Students were able to use guess and check, along with “balance reasoning”, to find the correct value.

 

 

The “mystery” of these problems can be ramped up rather easily and foster the need for a more sophisticated strategy.  I began having the students simply write the equation that could be represented by the mystery number equation.  The students had been wrapped up in the fact that these were at once so easy, but now not so much.  I used the mystery number problems written side by side with its algebraic representation in order to show the students how the “balance reasoning” related to the algebraic manipulation.

Students seemed to invest in this process because it was connected to something that they knew they could do.  I talked with them a lot about how math is all about learning more and more sophisticated ways to represent problems–even ones that they could do with an elementary level of understanding.  I believe it was the connection to a task that they found doable-that allowed them to find the algebra less intimidating.

Additionally, I used problems like this from Sarah Rubin.

I’m very interested in following the rest of the train of thought over at Problem Problems…

 

Everything I learned about teaching I learned from teaching students with special needs…

I came about a teaching career in a round about way.  As a math major at a small liberal arts college in Southern Maryland, I earned money by tutoring local middle and high school students.  I realized that I really enjoyed this experience and decided to pursue a teaching degree at the graduate level.

While taking classes towards a graduate degree for secondary math instruction, I fell into a job at a non-public special education facility.  I worked under a conditional certificate with some very wonderful special educators.  I ended up becoming THE math teacher for the entire high school program (the Harbour School is a k – 12 facility).  This meant that I taught all of the students ALL of their high school math.

I believe that I wouldn’t be the educator that I am today without this experience.

At the Harbour School I worked with students with all sorts of ABILITIES.  This school was their SAFE HARBOUR.  The students came to the school because it was found that their home school couldn’t meet their educational needs.

Teaching math at this school was an exercise in flexibility.  I had to really listen to the students to understand their understanding.  I do believe that math was a mystery for most.  I’ve always used this analogy for teaching math…

If I couldn’t get through the front door, I found a way in through the window, the garage, or around the back of the house.

By having to ask the right questions and make the right connections, this experience helped me to understand the math I was teaching at a deeper level.

At the Harbour School I also learned:

• acceptance
• tolerance
• patience
• community
• awareness
• perseverance
• resilience

If you are wondering about how to meet the needs of the students in your classroom with learning challenges–my advice is to listen to them.  ...Then figure out how to get into the house…

My favorite talk about listening from @maxmathforum…

#intenttalk Book Study Leads to Questions about Effective vs Efficient

I was inspired to coordinate the Intentional Talk book study this summer by a conversation between Tracy Zager and Dylan Kane.

@math8_teacher Have you read Intentional Talk by @ekazemi @allisonhintz124? Your desire for "deliberate decisions" is what they wrote to!

— Tracy Johnston Zager (@TracyZager) May 23, 2015

The Intentional Talk book study began in June with various people taking the lead–including the authors of the book Elham Kazemi and Allison Hintz.

Schedule for #intenttalk Chat will be slow chat style with a chapter per week, one question per day pic.twitter.com/HsTR1J8G8r

— Bridget Dunbar (@BridgetDunbar) June 16, 2015

This week, Allison Hintz posted a question that lead to a conversation about effective vs efficient strategies.  I tried to capture my current wonderings in this 140 character tweet:

@mary_dooms thinking of moving Ss along a continuum of more sophisticated algebraic representations…does that = more efficient #intenttalk

— Bridget Dunbar (@BridgetDunbar) July 14, 2015

At the end of this past school year I came across this task.

I worked with on-level 8th grade students this year, but as the school Instructional Resource Teacher, I spoke with our 7th Accelerated teachers and Algebra 1 teacher to see if they would be on board with giving this task to each of these cohorts.  All of the students had been taught systems of equations this year–but notice how unstructured and simply worded this task is.  I wondered what sort of strategies the students (at all of these various levels) would apply towards getting a solution for this task.  We used it to gauge the sort of student that would be appropriate for a 45 minute algebra class vs a 90 minute algebra class.

The range of approaches was very interesting to me. 

The following examples are from the 8th grade students that I worked with…I organized these student responses in the sort of continuum that occurred.  (Interestingly, the 7th accelerated and the Algebra 1 students didn’t have too dissimilar a range of solution strategies.)

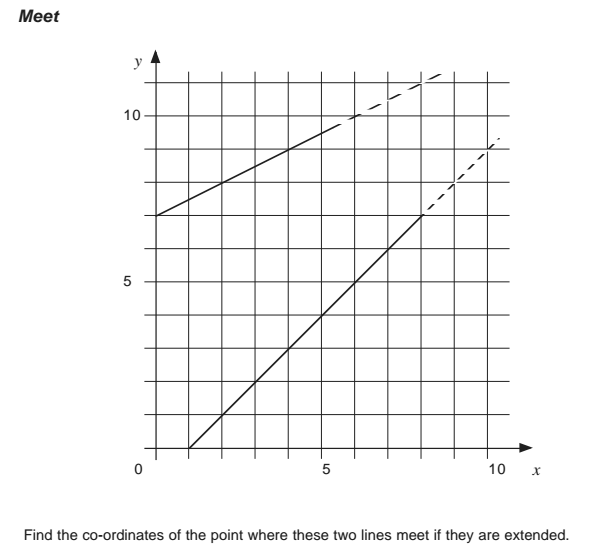
Students that chose graphing…

Student 1:  extended the lines but without precision or using any tools

Student 2:  asked for a ruler in order to extend the graph in a more precise fashion

Student 3:  asked for graph paper and created a graph using discrete points

Students that chose tables…

Student 4:  created two separate tables beginning at x = 0 and found the values that represented the intersection point

Student 5:  created a single table beginning at x = 10.  This student did not pull the correct information from graph to begin the table.

Students that wrote a one-variable equation…

Student 6:  wrote each linear equation and then used the substitution method to find the solution.  This student did have difficulty at the end because she struggled with what to do with (1/2)x = 8.  She eventually made sense of that part.

Student 7:  was able to use the substitution method to write the one-variable equation as well.  This student is not your typical top student and she was able to easily handle .5x=8.  I asked her if she used the calculator (which I had allowed) because she didn’t get stuck like a few other of the “smart” kids.  She said that she knew it took two groups of .5 to make 1 so she multiplied 8 by 2 and got 16.  It was amazing to me how it was so easy for her to flip to ratio reasoning when that last bit was a challenge for some of the “top” students.

This all leads me back to my original wondering…graphing, tables, equations were all effective methods (for some).  But, I am considering an efficient method to be one that utilizes grade level understandings and the goal should be to help students work through this continuum.

There has been a lot of discussion regarding the meaning of efficient.  Does this mean fast?  I think you are probably only able to use an efficient strategy if you have multiple strategies to choose from.  Otherwise, your ONE strategy is the effective/efficient strategy.

It’s important to give students these sort of unstructured tasks and let them figure out what they’d do on their own.  I would definitely use this task again and then use one of the targeted discussion strategies from Intentional Talk.